GD(ij) =0.137 log (pop (i)/pop (j)) + 0.145 log (y (i)/y (j)) + 0.739 log (exp (i)/exp (j))
The quants strike again.
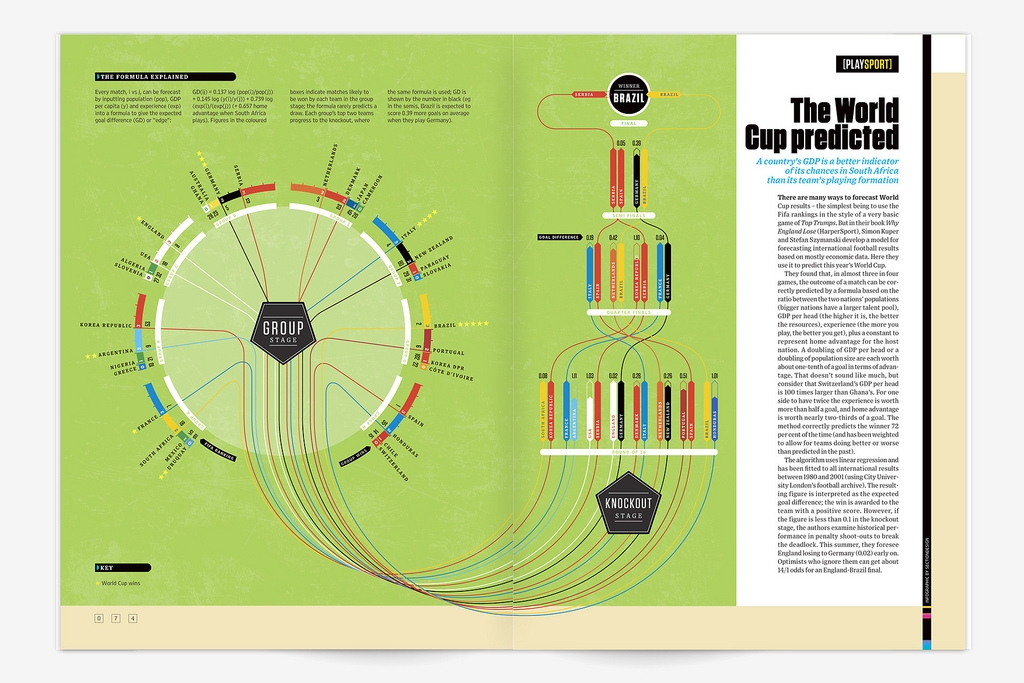
Simon Kuper and Stefan Szymanski have applied the following forecasting model they developed for their book “Why England Lose”![]() to the 2010 FIFA World Cup Tournament.
to the 2010 FIFA World Cup Tournament.
GD(ij) =0.137 log (pop (i)/pop (j)) + 0.145 log (y (i)/y (j)) + 0.739 log (exp (i)/exp (j))
Where i and j are the opposing sides.
“GD” is the goal difference between the two sides, “pop” = population, “y” = GDP per head and “exp” = team experience.
South Africa gets an additional 0.657 each game for home team advantage.
The above formula based on the ratio between the opposing team’s populations, GDP per person, experience and home field advantage for the host nation, Kuper and Syzmanski have applied linear regression (Huh?) to show that the outcome of international matches can be accurately predicted 72% of the time.
Their winner?
Brazil over Serbia.
Click the chart below for a larger, more readable version.
The chart was scanned from a ![]() Wired Magazine UK article at my other new favorite site, Chart Porn
Wired Magazine UK article at my other new favorite site, Chart Porn![]()
The favored matchup by the betting public is England v. Brazil at about 14/1.
The odds for a Serbia v. Brazil final currently stand at about 150/1.
I'm thinking about it for a hundred.
I might put another hundred on Spain, my favorite team, to win.
Why Spain?
England?
Lose
At least now we know why.















































![[Most Recent Quotes from www.kitco.com]](http://www.kitconet.com/charts/metals/gold/t24_au_en_usoz_2.gif)




![[Most Recent Quotes from www.kitco.com]](http://www.kitconet.com/charts/metals/silver/t24_ag_en_usoz_2.gif)





